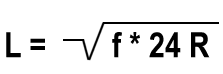Krzywe przejściowe w modelarstwie kolejowym

Wstęp

Odcinki proste i łukowe istnieją na każdej makiecie... ale:
bezpośrednie łączenie torów prostych z łukami nie jest zalecane z kilku powodów:
Dlatego najlepszym rozwiązanie tego problemu jest zastosowanie Krzywej Przejściowej (KP). Krzywa przejściowa, to nic innego jak płynne przejście z odcinka prostego torów w łuk. Takie rozwiązanie stosuje się przy mudowie makiet modułowych, które mają bardzo realistyczny wygląd (duże promienie łuków, długie odcinki torów szlakowych).
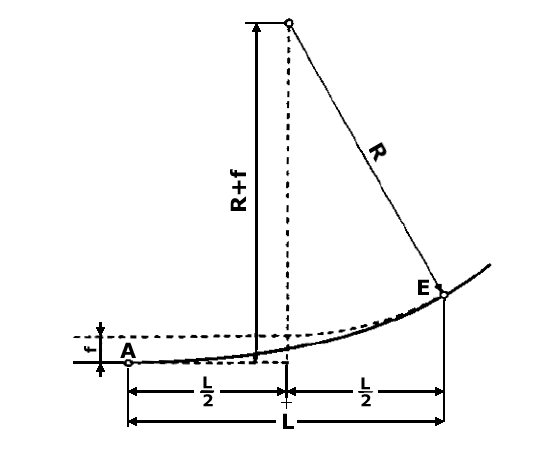
Rozmiar: 8377 bajtów
Przykład KP:

Najbardziej istotne w KP jest odległość f, która wyznacza przesunięcie osi toru przy realizacji krzywej. Prościej mówiąc odległość miedzy osią zakładanego toru bez użycia krzywej i osią toru rzeczywistego z użyciem tejże. (Idea krzywej polega na płynnym wzrastaniu wartości promienia łuku R, aż osiągnie wartość R+f) Wartość L wyznacza odległość między punktem A - koniec odcinka prostego i początek krzywej, a punktem E wyznaczającym koniec krzywej i początek odcinka łuku. Odległość f jest stała (ale nie zawsze, o tym poniżej) dla danego roztawu szyn G (skali) i wynosi:

tabela nr 1
G 6,5 9 12 16,5 22,5 32 45
f 3 4 6 9 13 18 25

Odległość L wylicza się przy pomocy następującego wzoru:
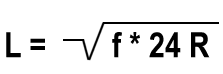
Rozmiar: 2129 bajtów
Dla standardowych promieni łuków przedstawiona została tabela nr 2. np. dla promienia łuku 1000 mm i rozstawie szyn 16,5 mm (H0) odległość L wynosi 465 mm.
tabela nr 2
G \ R 150 175 200 250 300 350 400 500 600 700 800 1000 1200 1400 1600 2000
6,5 100 110 120 135 145 160
9 130 140 155 170 185 195 220
12 190 210 225 240 270 295 320
16,5 275 295 330 360 390 415 465 509 550
22,5 395 430 465 500 560 610 660
32 550 590 655 720 780 830 930
45 775 850 915 980 1095

Ja wspomniano wcześniej, f jest dla danej skali stałe, lecz można także tą wartość wyliczyć odpowienim wzorem.
Trzeba jednak wcześnij sprawdzić stosunek L do R, dzieląc wartość L przez R (L / R) i dopiero wtedy w zależności od wyniku dobrać wzór z tabeli nr 3. np. 1000 / 465 co się równa 0,465, czyli istotny dla nas wzór, to ten pod wartością <0,6.

Tabela nr 3
L / R < 0,6 0,6 - 0,8 >0,8
f L2
24 R 		L2
23 R 		L2
22 R


Wyznaczanie współrzędnych składowych KP


Krzywą przejściową można wyznaczyć obliczając współrzędne punktów składowych krzywej.
W tym celu zakres długości L został podzielony na 10 części (nie korzystamy tutaj z 0,1 i 0,2 długości). Poszczególnym częściom xi odpowiadają wysokości yi krzywej. Wszystkie proporcje podane zostały w tabeli nr 4

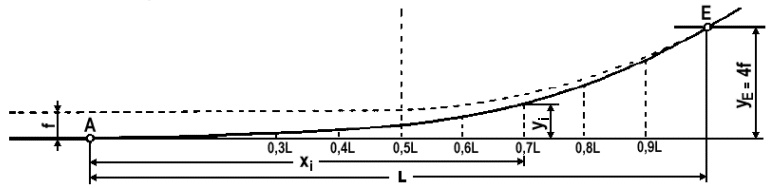
Rozmiar: 5007 bajtów


tabela nr 4
xi 0 0.3 L 0,4 L 0,5 L 0,6 L 0,7 L 0,8 L 0,9 L 1,0 L
yi 0 0.03 yE 0,06 yE 0,125 yE= 0,5f 0,21 yE 0,33 yE 0,49 yE 0,73 yE 1,0 yE =4f


Przykład wyliczania punktów krzywej xi i yi przy pomocy tabeli nr 4


roztaw szyn G = 16,5 mm
promień łuku R = 600 mm

Odczytaj wartość f z tabeli 1: f=9
Zakres długości krzywej L, tabela nr 2: L=360
Podstawmy yE = 4f = 36
Wyliczamy: xi = 0,7L odpowiada yi = 0,33yE
Wychodzi więc 0,33 * 36 = ~12
xi = 252 mm
yi = 12 mm


Wyznaczanie KP przy pomocy elastycznej sztaby


Istnieje ciekawa metoda wyznaczanie KP:
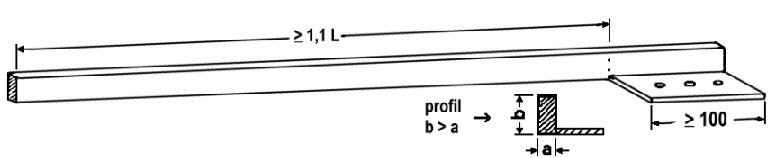
Można w tym celu użyć elastyczną sztabę (np. wykonaną z niezbyt grubej sklejki, drewniany liniał - można poeksperymentować) Trzeba tylko mieć możliwość przymocowania z jednego końca sztaby kątownika, za pomocą którego przykręcimy ją do podłoża. Wygląd sztaby przedstawia rys poniżej. Rozmiar: 13597 bajtów

Wymierzanie KP za pomocą szablonu
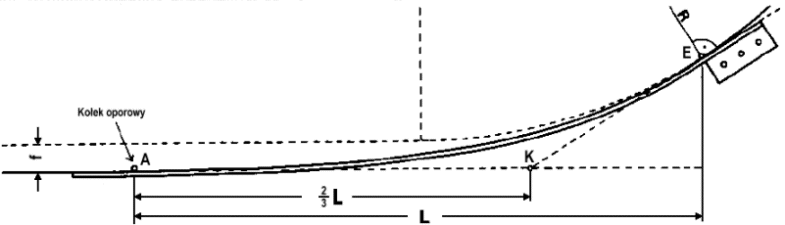
Najłatwiej będzie zacząć od prostej. Zaznaczamy punkt zakończenia prostej/początku krzywej A i rysujemy dalej linię o długości L. Następnie na końcu tej lini, pod kątem prostym rysujemy linię o długości 4f, której wierzchołkiem jest punkt E. Należy także wyznaczyć punkt K, leżący w odległości 2/3 L od punktu A. Teraz jedynie pozostało połączyc punkty K i E (przeciągając trochę poza E ).
W punktach A i E wbijamy kołki oporowe (np. gwoździe), przykręcamy sztabę wzdłuż lini K - E zwracając uwagę na zakończenie kształtownika mocującego sztabę (powinien kończyć się przy punktcie E tak jak na rysunku). Dociskamy teraz sztabę do kołka oporowego A i odrysowujemy krzywą.
Rozmiar: 13335 bajtów

Wyznaczanie KP przy pomocy programu graficznego Corel DRAW


Jeśli mamy wprawę posługiwania się Corelem, możemy to także wykorzystać.
Trzeba tylko wyrysować tak jak wyżej podałem w programie, a później zamiast sztaby, w Corelu używamy w tym celu narzędzia rysunek odręczny Rozmiar: 925 bajtów.
Punkty A i E łączymy przy pomocą prostej ze sobą, a następnie przekształcamy w krzywą. Pojawiają się wtedy linie pomocnicze, z których jedną przyginamy do prostej K - E (od punktu E) i kończymy w punktcie K a drugą doprowadzamy tylko do punktu A - ktrzywa gotowa.
Tutaj są rysunki poglądowe: pierwszy i drugi

Jarosław Dziub 2000

Zobacz też: Kreisbogen